Descriptive Statistics

This chapter draws on material from:

Introductory Statistics by OpenStax, licensed under CC BY 4.0
ModernDive by Chester Ismay and Albert Y. Kim, licensed under CC BY-NC-SA 4.0

Changes to the source material include light editing, adding new material, deleting original material, combining material, rearranging material, and adding first-person language from current author.

Introduction

Once you have collected data, what will you do with it? Data can be described and presented in many different formats. For example, suppose you are interested in buying a house in a particular area. You may have no clue about the house prices, so you might ask your real estate agent to give you a sample data set of prices. Looking at all the prices in the sample often is overwhelming. A better way might be to look at the median price and the variation of prices. The median and variation are just two ways that you will learn to describe data. Your agent might also provide you with a graph of the data.

In this chapter, you will study numerical (and graphical) ways to describe and display your data. This area of statistics is called "Descriptive Statistics." You will learn how to calculate, and even more importantly, how to interpret these measurements (and graphs).

Because we've already discussed visualizing data at length, we won't be revisiting too much of that in this chapter. However, as you consider the new material in this chapter, pay close attention to how what we've already learned about visualization relates to what we're learning now. Furthermore, we'll also cover a couple of kinds of visualization (stemplots and boxplots) that we haven't touched on yet. In the case of boxplots, you can't really appreciate their value without learning more about descriptive statistics, so we'll leave it for the end. In contrast, though, stemplots provide us with a great introduction to descriptive statistics, so that's where we'll start.

Stemplots and Describing Data

Stemplots (or the stem-and-leaf graph) comes from the field of exploratory data analysis. It is a good choice when the data sets are small. To create the plot, divide each observation of data into a stem and a leaf. The leaf consists of a final significant digit. For example, 23 has stem two and leaf three. The number 432 has stem 43 and leaf two. Likewise, the number 5,432 has stem 543 and leaf two. The decimal 9.3 has stem nine and leaf three. Write the stems in a vertical line from smallest to largest. Draw a vertical line to the right of the stems. Then write the leaves in increasing order next to their corresponding stem.

For example, let's imagine that scores for the first exam in a pre-calculus were as follows (smallest to largest): 33; 42; 49; 49; 53; 55; 55; 61; 63; 67; 68; 68; 69; 69; 72; 73; 74; 78; 80; 83; 88; 88; 88; 90; 92; 94; 94; 94; 94; 96; 100.

Stem	Leaf
3	3
4	2 9 9
5	3 5 5
6	1 3 7 8 8 9 9
7	2 3 4 8
8	0 3 8 8 8
9	0 2 4 4 4 4 6
10	0

The stemplot shows that most scores fell in the 60s, 70s, 80s, and 90s. Eight out of the 31 scores or approximately 26% (8/31) were in the 90s or 100, a fairly high number of As.

The stemplot is a quick way to graph data and gives an exact picture of the data. You want to look for an overall pattern and any outliers. An outlier is an observation of data that does not fit the rest of the data. It is sometimes called an extreme value. When you graph an outlier, it will appear not to fit the pattern of the graph. Some outliers are due to mistakes (for example, writing down 50 instead of 500) while others may indicate that something unusual is happening. It takes some background information to explain outliers, so we will cover them in more detail later.

A stemplot may seem cruder than the kinds of visualization that we've touched on so far—in fact, it's tricky to fit this into the grammar of graphics that we used to describe previous plots. However, I'm bringing it up here because as crude as it is, it's also obviously and immediately useful. Without even using ggplot2, we already have a visual indication of patterns in the data, including any outliers that we might need to look into. We get an immediate, intuitive impression of the location of the data that we're looking at.

Percentiles

However, a stemplot is really only practical for (very) small datasets. It's great to demonstrate why we value data visualization, but it's not practical in many cases. With a larger dataset (and with access to software like R), it's probably easier to measure the location of data with some quantitative techniques, like quartiles and percentiles.

To calculate quartiles and percentiles, the data must be ordered from smallest to largest. Quartiles divide ordered data into quarters. Percentiles divide ordered data into hundredths. From this, it should be clear that quartiles are, in fact, special percentiles. The first quartile, Q1, is the same as the 25th percentile, and the third quartile, Q3, is the same as the 75th percentile. The median, M or Q2, is called both the second quartile and the 50th percentile.

To score in the 90th percentile of an exam does not mean, necessarily, that you received 90% on a test. It means that 90% of test scores are the same or less than your score and 10% of the test scores are the same or greater than your test score. Percentiles are mostly used with very large populations. Therefore, if you were to say that 90% of the test scores are less (and not the same or less) than your score, it would be acceptable because removing one particular data value is not significant.

However, this also reminds me of the time that I saw a pediatric nurse write down "100th" percentile on the chart for a baby who was even taller than the 99th percentile value that the nurse had been given. The nurse had never seen a baby of that sex so tall before and was understandably impressed, but can you see why "100th" percentile doesn't work here? Even if we used a more conservative interpretation, we'd still be arguing that 100% of babies of that sex in the U.S. are the same height or shorter than this baby. As tall as this baby was, the data didn't support that conclusion. However, you may run into references to a 100th percentile (or Q4) when someone is indicatng the highest value in a dataset.

The Median and Quartiles

The median is a number that measures the "center" of the data. You can think of the median as the "middle value," but it does not actually have to be one of the observed values. It is a number that separates ordered data into halves. Half the values are the same number or smaller than the median, and half the values are the same number or larger. For example, consider the following data:

1; 11.5; 6; 7.2; 4; 8; 9; 10; 6.8; 8.3; 2; 2; 10; 1

Ordered from smallest to largest:

1; 1; 2; 2; 4; 6; 6.8; 7.2; 8; 8.3; 9; 10; 10; 11.5

Since there are 14 observations, the median is between the seventh value, 6.8, and the eighth value, 7.2. To find the median, add the two values together and divide by two.

Thus, the median is seven (6.8 plus 7.2 equals 14; 14 divided by 2 is 7). Half of the values are smaller than seven and half of the values are larger than seven.

Quartiles are numbers that separate the data into quarters. Quartiles may or may not be part of the data. To find the quartiles, first find the median or second quartile. The first quartile, Q1, is the middle value of the lower half of the data, and the third quartile, Q3, is the middle value, or median, of the upper half of the data. To get the idea, consider the same data set:

1; 1; 2; 2; 4; 6; 6.8; 7.2; 8; 8.3; 9; 10; 10; 11.5

We've already established that the median or second quartile is seven. The lower half of the data are:

1, 1, 2, 2, 4, 6, 6.8

The first quartile (the middle value of the lower half) is two. Note that unlike the median, the first quartile is an actual value in the data. One-fourth of the entire sets of values are the same as or less than two and three-fourths of the values are more than two.

The upper half of the data is:

7.2, 8, 8.3, 9, 10, 10, 11.5

The third quartile, Q3, is nine. Three-fourths (75%) of the ordered data set are less than nine. One-fourth (25%) of the ordered data set are greater than nine. The third quartile is part of the data set in this example.

The interquartile range is a number that indicates the spread of the middle half or the middle 50% of the data. It is the difference between the third quartile (Q3) and the first quartile (Q1).

IQR = Q3 – Q1

The IQR can help to determine potential outliers. One rule of thumb is to treat a value as a potential outlier if it is less than 1.5 * IQR below the first quartile or more than 1.5 * IQR above the third quartile. However, as widespread as this advice is, it's still just a rule of thumb. Potential outliers always require further investigation.

Finding Percentiles and Quartiles in R

One important thing to learn about R is that there are nearly always multiple functions that will do the same (or at least similar) things for you. Sometimes, choosing a package from among these different options is just a matter of preference; other times, there are strong reasons (often based on small, technical details) to prefer one over the other. Let's look at two functions that you can use in R for finding percentiles and quartiles (and, often, other information besides).

fivenum()

The fivenum() function, as the name suggests, returns five descriptive numbers: The minimum value, the 25th percentile (Q1), the 50th percentile (Q2 or the median), the 75th percentile (Q3), or the maximum value (the 100th percentile or Q4). One of my favorite example datasets in the tidyverse package is starwars, so let's use that as an example of how to use fivenum():

starwars %>% select(mass) %>% fivenum()

# [1] 15.0 55.6 79.0 84.5 1358.0

Note how I'm using %>% pipes to structure my code here. I'm beginning with a named dataset, starwars, which is preloaded in tidyverse—so long as I have library(tidyverse) earlier in my code, I don't have to import or define the dataset elsewhere. If I were to look over the starwars dataset (using, for example, starwars %>% View() (to see all the data) or starwars %>% head() (to see the column names and first few rows) , I'd see that this is a data set of Star Wars characters and demographic characteristics about them. So, I use the select() function to grab a numeric variable (obviously, we can't calculate percentiles and quartiles for categorical variables)—in this case, mass—and then pipe that into fivenum().

The second code chunk—my results—don't have a lot of output with them, so it's up to me to remember what the numbers mean (or check the help for this function with ?fivenum() to remind myself). It looks like the minimum mass for the Star Wars characters in this data set is 15 kg, the median is 79 kg, and the maximum is 1,358 kg (spoiler: it's Jabba the Hutt), with Q1 and Q3 filling in the gaps.

quantile()

This function is a bit more finicky but can also be more helpful. Let's use the same dataset to show how this works:

starwars %>% select(mass) %>% quantile(na.rm = TRUE)

# 0% 25% 50% 75% 100% 15.0 55.6 79.0 84.5 1358.0

My input and output are both pretty similar to fivenum(), but there are some important differences. First, I've had to include an extra argument in quantile(): na.rm = TRUE. This argument is short for "NA remove." NA is a special value in R that means not applicable; for example, as dedicated as Star Wars nerds can be, we just don't have canonical mass values for certain characters in the franchise; so, we put an NA in instead as a sort of "blank" value. We can't put a 0 in there because that would do things like mess with percentiles and quantiles without our being aware of it; however, we also can't calculate percentiles and quantiles when NAs are in there either, because NA isn't a quantitative value. If we try to run this code without na.rm = TRUE, we'll get a big fat error, but by including the argument, quantile() knows to remove any NA values before doing its math.

So, why don't we have to do this for fivenum()? Well, the truth is that we do, but fivenum() automatically assumes that we want to remove NAs and quantile() doesn't. You can learn some of these nitty gritty details by opening the help files for these functions (by running ?fivenum() and then ?quantile()) and reading more about them; in this class, you generally won't have to get into the weeds about a function before using it, but as you venture on your own, it's really important and useful to read the documentation for functions that you rely on.

The other difference to notice here is that quantile() gives us a bit more output than fivenum() did. While we had to remember what the numbers in fivenum() represented, quantile() tells us. There's actually a pretty important reason behind this, and that's related to the reason we might consider using quantile() instead of fivenum(). Take a look at the code and output below: Can you see what I've done differently?

starwars %>% select(mass) %>% quantile(probs = c(0,.33,.66,1.00),na.rm = TRUE)

# 0% 33% 66% 100% 15.0 68.84 82.00 1358.0

Hopefully you've been able to puzzle this out on your own, but let's walk through it together. Remember that quartiles are a particular kind of percentiles: Just because quantiles are widely used doesn't mean that percentiles aren't more useful sometimes. By adding the argument probs = c(0,.33,.66,1.00), I've told quantile() that I don't want quartiles: I want the minimum value, the 33rd quartile, the 66th quartile, and the maximum value. Essentially, I'm splitting things up into thirds rather than quarters, and the output reminds me of that!

Now, do I have a compelling theoretical reason to divide Star Wars characters into three groups by mass? Not really—but quantile() lets me do that if I want to, and there are times when I will want to.

Interpreting Percentiles, Quantiles, and Median

A percentile indicates the relative standing of a data value when data are sorted into numerical order from smallest to largest. Percentages of data values are less than or equal to the pth percentile. For example, 15% of data values are less than or equal to the 15^th percentile.

Low percentiles always correspond to lower data values.
High percentiles always correspond to higher data values.

A percentile may or may not correspond to a value judgment about whether it is "good" or "bad." The interpretation of whether a certain percentile is "good" or "bad" depends on the context of the situation to which the data applies. In some situations, a low percentile would be considered "good;" in other contexts a high percentile might be considered "good". In many situations, there is no value judgment that applies.

Understanding how to interpret percentiles properly is important not only when describing data, but also when calculating probabilities in later chapters of this text.

Boxplots

Now that we've talked about percentiles and quartiles, it's time to come back to another data visualization technique: the boxplot. Think back to when we used a histogram to visualize the different temperatures measured at New York City airports:

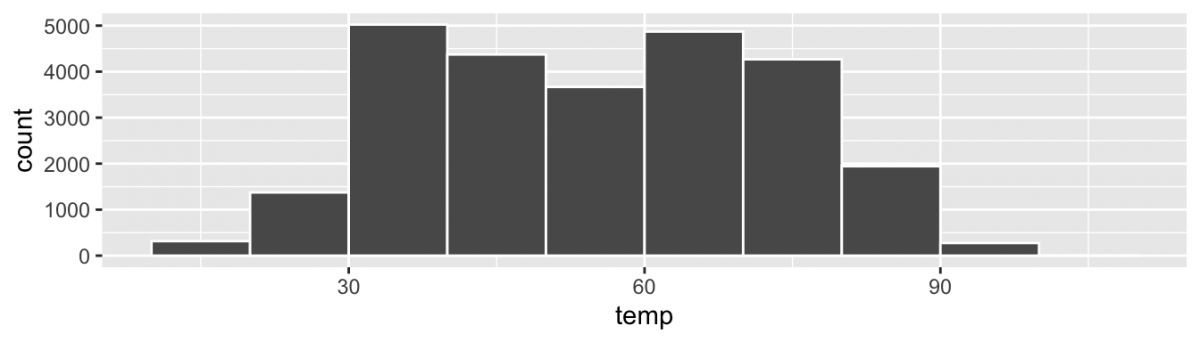This histogram is legitimately helpful for exploring the location of these data; however, now that we've learned about percentiles and quartiles, it's time to talk about how we can combine those quantitative measures with data visualization to harness the power of both!

Let's back up even further than histograms and look at a scatterplot; to keep things simple for now, let’s only consider the 2141 hourly temperature recordings for the month of November, each represented as a jittered point.

This is kind of a mess—it's not a great scatterplot at all—but I'm including it here to contrast it with a much better boxplot that's about to come!

Now, thanks to fivenum() (or quantile()), it would be pretty easy for us to figure out the following values for these data:

Minimum: 21°F
Q1 (25th percentile): 36°F
Median (Q2, 50th percentile): 45°F
Q3 (75th percentile): 52°F
Maximum (Q4; 100th percentile): 71°F

In the figure below, we're going to use these numbers to transition from terrible scatterplot to helpful boxplot. On the leftmost plot, we'll add the fivenum() values with dashed horizontal lines on top of the 2141 points. In the middle plot,we'll add the boxplot. Then, in the rightmost plot we'll remove the points and the dashed horizontal lines for clarity’s sake:

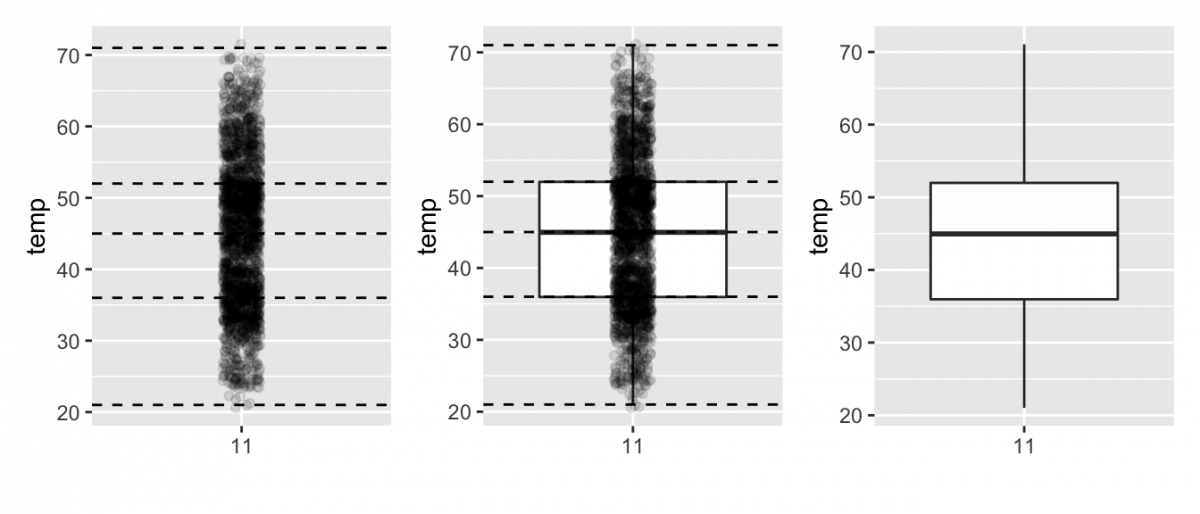As you can see from this figure, what the boxplot does is visually summarize the 2141 points by cutting the 2141 temperature recordings into quartiles at the dashed lines, where each quartile contains roughly 2141 $\div$ 4 $\approx$ 535 observations. Thus

25% of points fall below the bottom edge of the box, which is the first quartile of 36°F. In other words, 25% of observations were below 36°F.
25% of points fall between the bottom edge of the box and the solid middle line, which is the median of 45°F. Thus, 25% of observations were between 36°F and 45°F and 50% of observations were below 45°F.
25% of points fall between the solid middle line and the top edge of the box, which is the third quartile of 52°F. It follows that 25% of observations were between 45°F and 52°F and 75% of observations were below 52°F.
25% of points fall above the top edge of the box. In other words, 25% of observations were above 52°F.
The middle 50% of points lie within the interquartile range (IQR) between the first and third quartile. Thus, the IQR for this example is 52 - 36 = 16°F. The interquartile range is a measure of a numerical variable’s spread.

Furthermore, in the rightmost plot, we see the whiskers of the boxplot. The whiskers stick out from either end of the box all the way to the minimum and maximum observed temperatures of 21°F and 71°F, respectively. However, the whiskers don’t always extend to the smallest and largest observed values as they do here. They in fact extend no more than 1.5 * $\times$ from either end of the box. This should sound familiar! Any observed values outside this range are suspected to be outliers and get marked with points.

Here's another boxplot that marks outliers in that way; it also takes a look at all twelve months of the year, in a way that really demonstrates the power of quantiles and boxplots:

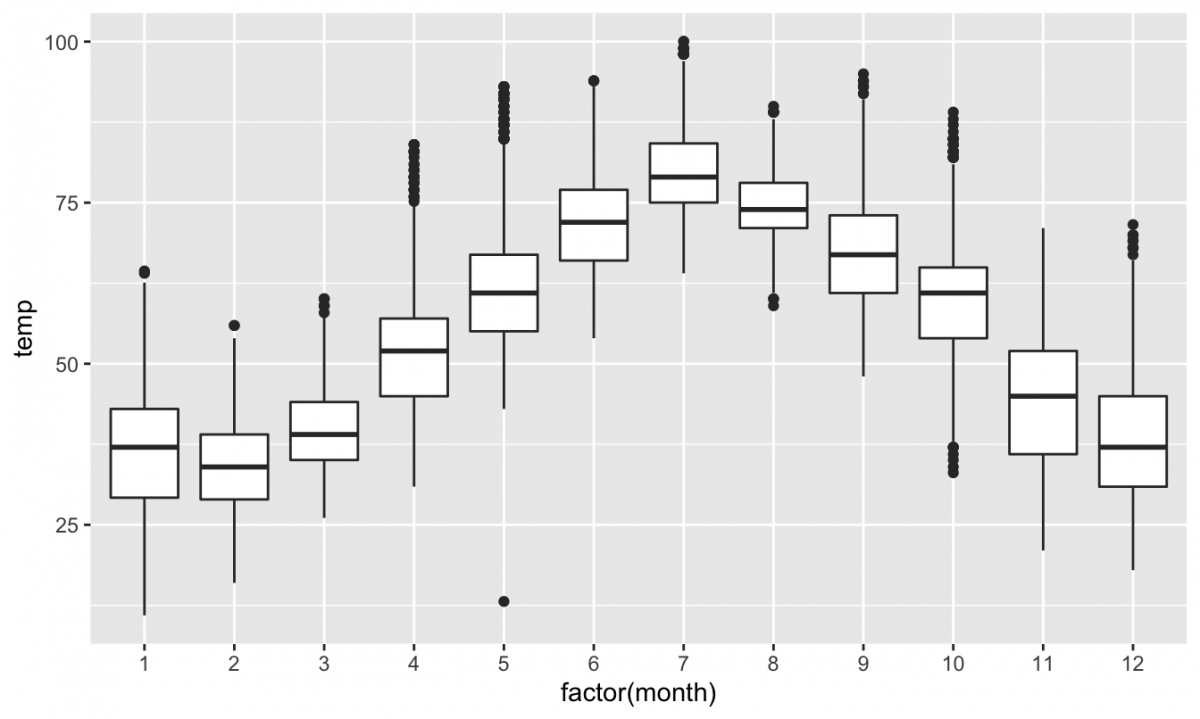
Spend some time exploring this plot. Remind yourself what the different elements of each boxplot represent in terms of quartiles, percentiles, etc. Remind yourself what quartiles and percentiles themselves mean! What conclusions can you draw or questions can you raise about these data based on this visualization?

Measures of Centrality

As you looked over the boxplot above, one thing you probably paid attention to was the line representing the median; it's natural to know what the "middle" value in a dataset is, and the median provides us with one way of doing so.

What we're doing when we're looking at the median is trying to find the "center" of a dataset, another important way of describing location. The median is one of the two mostly widely used measures of the "center" of the data, with the other being the mean (commonly referred to as the average). To find the median mass of 50 Star Wars characters, we would order the data and find the number that splits the data into two equal parts. To calculate the mean mass of 50 Star Wars characters, we would add the 50 masses together and divide by 50 (or, in R, feed the numbers in question into the mean() function.

The mean is the most common measure of the center; in my experience, people outside of the world of data, science, and data science rarely think to use the median instead. However, when there are extreme values or outliers, the median is generally a better measure of the center when there are extreme values or outliers. This is because the median is not affected by the precise numerical values of the outliers. If you remember from earlier, our max mass value from the Star Wars dataset was 1358 kilograms, thanks to the massive slug-like alien Jabba the Hutt. That's an extreme value, though (second place is General Grievous's mere 216 kg), and it's going to throw off any averages that we calculate: In fact, the mean mass of Star Wars characters is 97.31 kg, quite a bit more than the median of 79 kg. Data scientists know to check both measures of centrality!

Another measure of the center is the mode: the most frequent value. The mean is the most common measure of the center.

Skewness

Consider the following data set:

4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

This data set can be represented by following histogram:

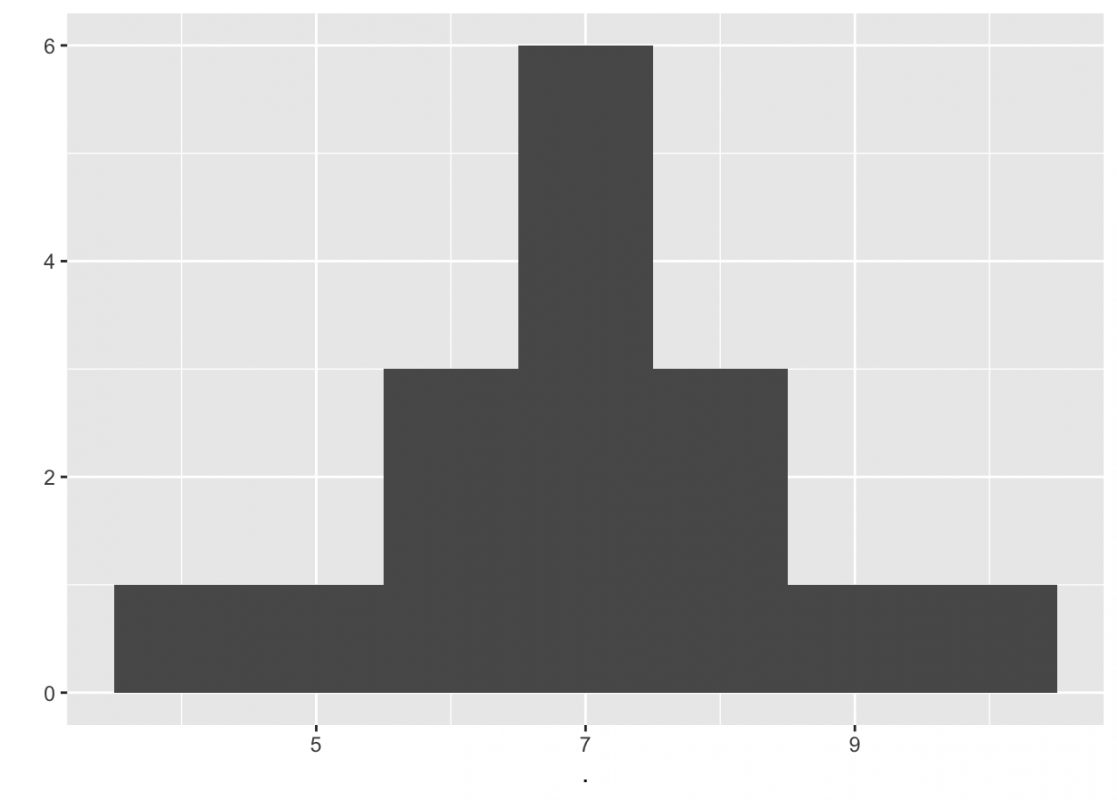
The histogram displays a symmetrical distribution of data. A distribution is symmetrical if a vertical line can be drawn at some point in the histogram such that the shape to the left and the right of the vertical line are mirror images of each other. The mean, the median, and the mode are each seven for these data. This example has one mode (unimodal), and the mode is the same as the mean and median. In a symmetrical distribution that has two modes (bimodal), the two modes would be different from the mean and median. In a perfectly symmetrical distribution, the mean and the median are the same. What does this tell us about the mass variable recorded in the starwars dataset?

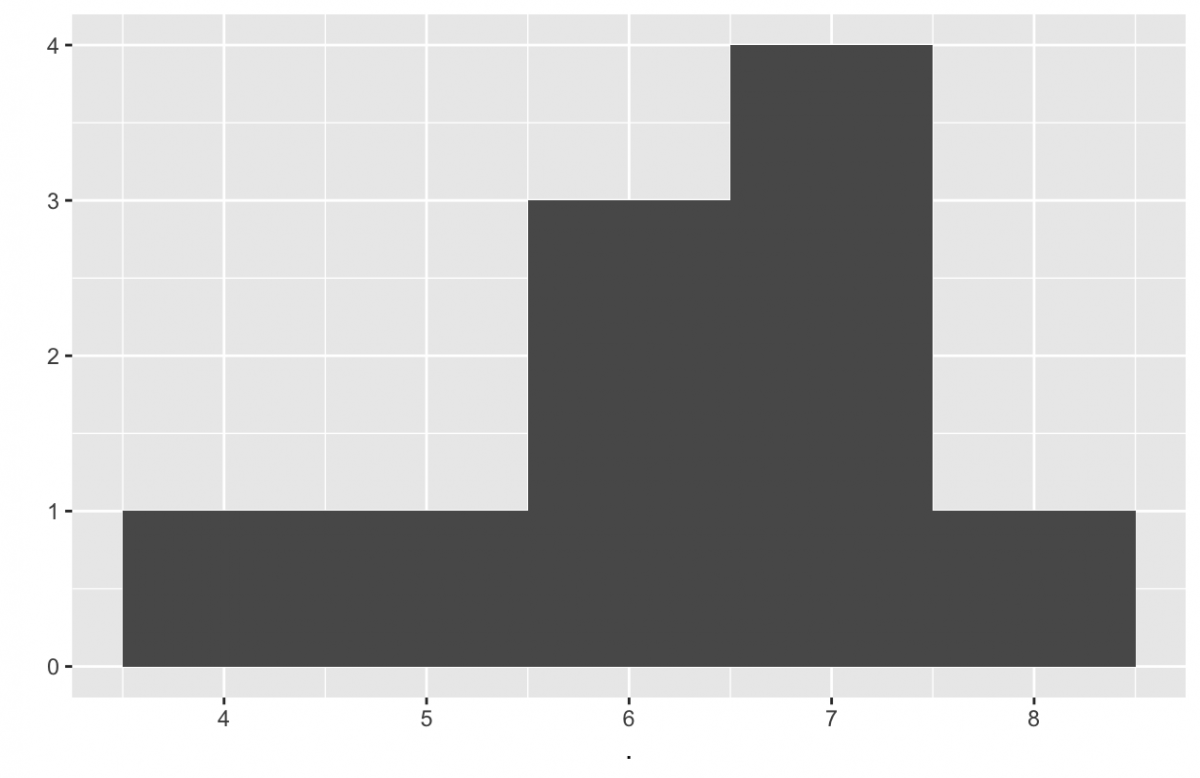
The histogram for the data 4; 5; 6; 6; 6; 7; 7; 7; 7;8 (seen above) is not symmetrical. The right-hand side seems "chopped off" compared to the left side. A distribution of this type is called skewed to the left because it is pulled out to the left. The mean is 6.3, the median is 6.5, and the mode is seven. Notice that the mean is less than the median, and they are both less than the mode. The mean and the median both reflect the skewing, but the mean reflects it more so.

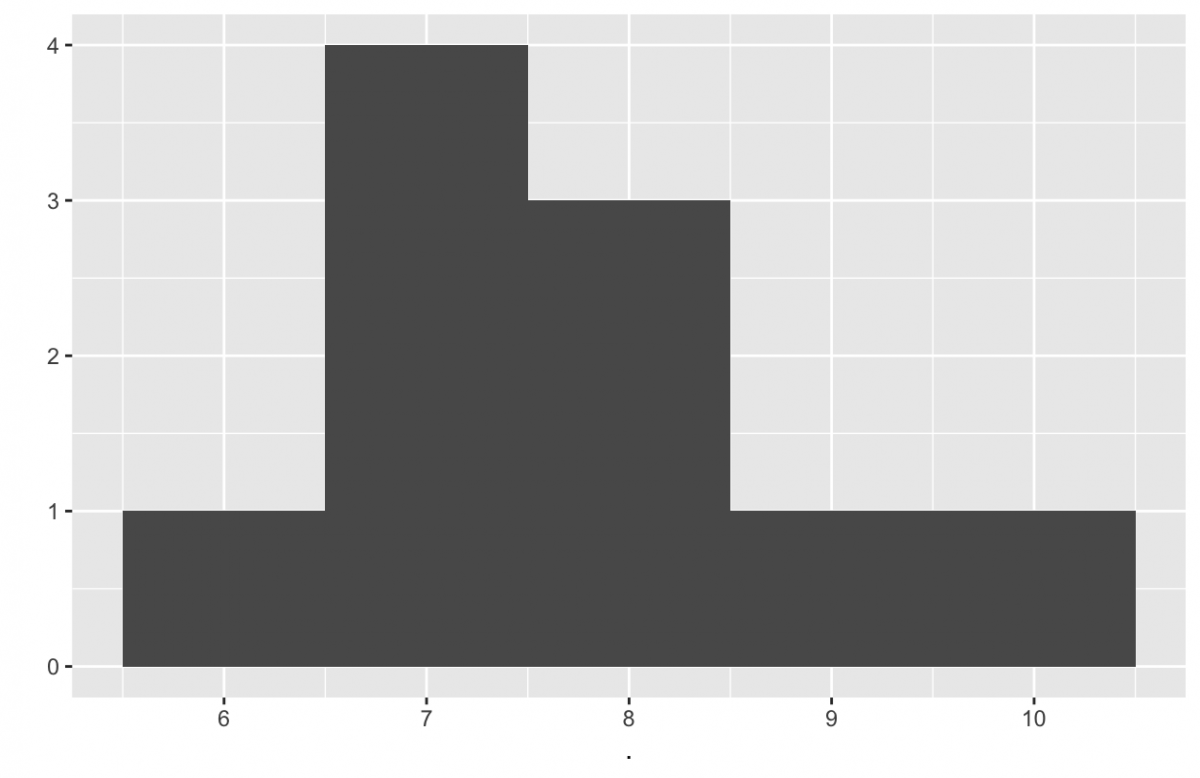
The histogram for the data: 6; 7; 7; 7; 7; 8; 8; 8; 9; 10 is also not symmetrical. It is skewed to the right. The mean is 7.7, the median is 7.5, and the mode is seven. Of the three statistics, the mean is the largest, while the mode is the smallest. Again, the mean reflects the skewing the most.

The mean is affected by outliers that do not influence the median. Therefore, when the distribution of data is skewed to the left, the mean is often less than the median. When the distribution is skewed to the right, the mean is often greater than the median. What does this tell us about Jabba the Hutt and our starwars data set? In symmetric distributions, we expect the mean and median to be approximately equal in value. This is an important connection between the shape of the distribution and the relationship of the mean and median. It is not, however, true for every data set. The most common exceptions occur in sets of discrete data.

Skewness and symmetry are important for learning about our data. For example, in my early social media research, it was common for me to calculate measures of participation, such as the number of tweets per participant in a specific hashtag. It was easy to calculate a mean and put that in the paper, but that usually didn't tell the whole story. Perhaps unsurprisingly, measures of activity in online communities (like tweets per participant) are typically skewed wayyyy to the right. Most participants aren't all that active, so most people are going to cluster at the "low" end of any histogram; however, there are always a few eager beavers that post a lot more than anyone else, pulling the right end of the histogram way out in that direction. In this case, the skewness itself told me a lot about what I was studying: There were a small number of very active participants in these communities, but most people had a more casual relationship with the online space.

Measures of Spread

An important characteristic of any set of data is the variation in the data. In some data sets, the data values are concentrated closely near the mean; in other data sets, the data values are more widely spread out from the mean. The most common measure of variation, or spread, is the standard deviation. The standard deviation is a number that measures how far data values are from their mean, and it is useful in two main ways:

Measure of the Overall Variation

The standard deviation provides a measure of the overall variation in a data set. The standard deviation is always positive or zero. The standard deviation is small when the data are all concentrated close to the mean, exhibiting little variation or spread. The standard deviation is larger when the data values are more spread out from the mean, exhibiting more variation.

Suppose that we are studying the amount of time customers wait in line at the checkout at supermarket A and supermarket B. the average wait time at both supermarkets is five minutes. At supermarket A, the standard deviation for the wait time is two minutes; at supermarket B the standard deviation for the wait time is four minutes.

Because supermarket B has a higher standard deviation, we know that there is more variation in the wait times at supermarket B. Overall, wait times at supermarket B are more spread out from the average; wait times at supermarket A are more concentrated near the average.

Measure of Distance from the Mean

The standard deviation can be used to determine whether a data value is close to or far from the mean. Suppose that Rosa and Binh both shop at supermarket A. Rosa waits at the checkout counter for seven minutes and Binh waits for one minute. At supermarket A, the mean waiting time is five minutes and the standard deviation is two minutes. The standard deviation can be used to determine whether a data value is close to or far from the mean.

Rosa waits for seven minutes:

Seven is two minutes longer than the average of five; two minutes is equal to one standard deviation.
Rosa's wait time of seven minutes is two minutes longer than the average of five minutes.
Rosa's wait time of seven minutes is one standard deviation above the average of five minutes.

Binh waits for one minute.

One is four minutes less than the average of five; four minutes is equal to two standard deviations.
Binh's wait time of one minute is four minutes less than the average of five minutes.
Binh's wait time of one minute is two standard deviations below the average of five minutes.

A data value that is two standard deviations from the average is just on the borderline for what many statisticians would consider to be far from the average. Considering data to be far from the mean if it is more than two standard deviations away is more of an approximate "rule of thumb" than a rigid rule. In general, the shape of the distribution of the data affects how much of the data is further away than two standard deviations. We'll come back to this later in the semester.

Calculating the Standard Deviation

If x is a number, then the difference "x – mean" is called its deviation. In a data set, there are as many deviations as there are observations in the data set. The deviations are used to calculate the standard deviation.

The procedure to calculate the standard deviation is technically different depending on specific characteristics about your data. However, we haven't yet covered the statistical concepts that inform that difference, and in practice, one of the two possible calculations is used in the overwhelming majority of cases. With that in mind, we're going to cover one calculation, but it's worth noting that this is one of two ways of calculating a standard deviation.

To calculate the standard deviation, we need to calculate the variance first. The variance is the average of the squares of the deviations. That is, we calculate the deviation for each observation in the dataset (using the math described above), square each deviation, and add them all together. For an average, we would normally divide that sum by the number of observations, and in some cases we do! However, as mentioned above, there are two ways of calculating a standard deviation, and with the way that we're doing things now, we do things slightly differently. We actually divide the summed squares of the deviations by the number of observations minus one. Then, we have our variance!

There's one problem with the variance, though. Calculating a deviation simply involves subtracting a mean value for a variable from each observed value of that variable, so a deviation is in the same units as the original variable. However, once we square all of those deviations as part of calculating the variance, we throw the scale off, and so we can't interpret variance in the same way that we would calculate deviations—or the original observations. This squaring is actually solving a different problem (positive and negative deviations would cancel each other out if we didn't make them all positive by squaring them), but it makes variance unintuitive to work with.

So, we need one additional step to convert unintuitive variance to more-intuitive standard deviation. Fortunately, it's an easy one: We just take the square root of the variance, and voilà: a standard deviation!

The standard deviation is either zero or larger than zero. Describing the data with reference to the spread is called "variability". When the standard deviation is zero, there is no spread; that is, the all the data values are equal to each other. The standard deviation is small when the data are all concentrated close to the mean, and is larger when the data values show more variation from the mean. When the standard deviation is a lot larger than zero, the data values are very spread out about the mean; outliers can make standard deviations very large.

The standard deviation is particularly useful when comparing data values that come from different data sets. If the data sets have different means and standard deviations, then comparing the data values directly can be misleading.

The standard deviation, when first presented, can seem unclear. By graphing your data, you can get a better "feel" for the deviations and the standard deviation. You will find that in symmetrical distributions, the standard deviation can be very helpful but in skewed distributions, the standard deviation may not be much help. The reason is that the two sides of a skewed distribution have different spreads. In a skewed distribution, it is better to look at the first quartile, the median, the third quartile, the smallest value, and the largest value. Because numbers can be confusing, always graph your data: Histograms and box plots are particularly useful.